平衡自行车-理论篇
标签:DIY 机器人
nicekwell 发布于 2018-01-22 00:51
Step 1: 模型分析




1、倒立摆
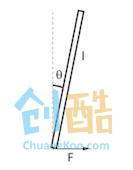
很显然我们知道自行车在左右方向上不稳定,这是一个很常见的物理模型——倒立摆。如上图1。
顾名思义,倒立摆的意思就是倒着的摆,比如一个倒着的杆,如上图2。
倒立摆的特性:不稳定,只要偏离平衡位置,就会有一个力(重力的分力)使系统更加偏离平衡位置,这样偏差就会越来越大。
一般倒立的杆在前后左右方向都有可能倒下,在二维的平面上不稳定;而自行车仅在左右方向上可能倒下,是一维的倒立摆,这要简单一些。
上图是几个生活中常见的倒立摆例子。
2、自行车的平衡控制
自行车属于倒立摆模型,倒立摆是不稳定的,那么倒立摆应该如何控制才能平衡呢?
我们把问题拆分一下:
- 怎样的状态才叫平衡?
- 我们能控制的是什么?
- 如何控制才能稳定平衡?
2.1 怎样的状态才叫平衡
我们要对”平衡”进行数学描述,所谓的平衡其实就是倒立摆的倾角稳定在一个我们想要的值。
如上图2,通常我们想要平衡在θ = 0处。
2.2 我们能控制的是什么
对于倒立摆模型,通常我们能控制的是底端的 力 或 速度 或 位置,不同的控制量对应的控制方法不同。
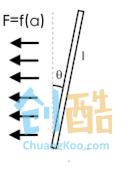
对于自行车来说,它的控制方式不像通常的倒立摆那样直接控制底部,而是间接地通过转向来控制,当自行车以一个固定的速度前进时,自行车把手以一定角度进行转向(设为α),自行车会做相应半径的圆周运动,产生相应大小的”离心力”。
在自行车这个费惯性系里看来,只要对把手进行一定角度的转向(α),就会产生一个相应大小的横向力,如上面最后一图。
这就是我们进行平衡控制时的实际控制量——把手转角α,只要控制它就能控制回复力。
2.3 如何控制才能平衡
上面我们已经能够通过转向产生回复力,这个回复力可以把倒立摆”掰回”平衡位置,有往回掰的回复力就能稳定平衡了吗?
并不是这样,我们再来回顾一下中学物理:
过阻尼状态的摆会以较慢的速度回到平衡位置;
欠阻尼状态的摆会很快回到平衡位置,但会在平衡位置来回摆动;
临界阻尼状态的摆会以最快的速度稳定在平衡位置。
结合到实际的自行车平衡中就是:
如果回复力不够大,就无法矫正,或者矫正速度很慢,这会导致系统不稳定;
如果回复力过大,就会导致矫正过度,这也会导致系统不稳定; 我们最希望的状态就是回复力刚刚好,刚好使倒立摆快速回到平衡位置,又不至于矫正过度。
这是一个复杂的数学计算过程,回复力大小会在系统运行时不断地计算(本平衡自行车是20ms计算一次),用到的是PID算法,会在后面详细介绍。
3、自行车平衡需要解决的基本问题
- 获取左右方向倾角θ
- 以合适的算法控制转角α使系统稳定平衡
这将会在下面详细讨论。
Step 2: 姿态检测
用一个叫gy521的模块,里面用的是mpu6050芯片,带有陀螺仪和加速度传感器。 gy521的具体使用会在第三篇 实践篇介绍,这里我们知道通过这个模块我们可以得到自行车各个方向的加速度和角速度。 注意哦,我们不能直接得到倾斜角度,我们的到的是各个方向的加速度和角速度,需要进行一些复杂的计算才能得到正确的倾斜角度。
常用的算法有互补平衡滤波、卡尔曼滤波,由于篇幅和精力问题这部分暂不介绍,网上有大量资源,也可以查看本工程源码,以后有时间再写详细教程。
Step 3: PID算法

前面已经分析了,我们通过控制把手转角来控制回复力,我们需要实时计算一个合适的回复力使系统稳定平衡。
这部分内容也不做详细介绍了,网上有大量资源,也可以查看本工程源码。
在这里引用动力老男孩举的一个例子,帮大家简单理解一下需要解决的问题,以及PID算法是如何解决的。
如上图,有一个小球在光滑球面上,小球的位置是x,光滑球面顶端在L处,我们可以控制小球水平方向力F,现在要求让小球稳定平衡在x0处。
先看简单情况 x0=L,此时偏差为 x-L,
我们给出一个比例项(P) F = kp*(L-x),这样就会有一个回复力,当偏差存在时就会有一个力把小球拉回L处。
这存在的问题是,小球接近L时是会有一定速度的,小球越来越接近L,此时的力仍然是在把小球往L处拉,这会导致小球到达L时(我们想要的位置)速度很大,小球无法立刻停下来,而是会冲过去。
这样小球就会在L附近来回摆动,这是不稳定的状态,属于欠阻尼状态。
为了解决上述问题需要加一个微分项(D) F = kd*dx/dt = kd*v,所谓”微分”指的是位置x对时间的微分,说白了就是速度。
意思就是当速度越大,就产生一个反向的力使速度减小,这样就可以防止出现上面小球冲过去的。
可以认为这一项具有”预测”功能,预测小球下一时刻的状态从而提前做出反应(预测小球将要到达L处,提前减速),
也可以认为这一项具有阻尼作用,相当于系统中有一个和速度成比例的阻尼力。
这个”阻尼力”调得过小会导致欠阻尼状态,调得过大会导致过阻尼状态。
积分项此时可以不用,积分项是当平衡位置x0不等于L时使用的,
当平衡位置不是L处,那么当小球静止在平衡位置x0时,由于在坡道上会有一个恒定的横向偏移力,此时比例调节作用为0(Δx=0),微分调节作用也是0(v=0),所以小球在该处无法平衡,会在更远离平衡位置处达到平衡,那么就会有一个长时间存在的偏差。
积分作用就是检测偏差进行累积,对于上面这个长时间存在的偏差进行积分(累积叠加),使系统在长时间范围可以稳定在要求的平衡位置。
Step 4: 广告



